Learning Archive

Small Signal Analysis of BJT

This section might summarizes the small signal analysis of a Bipolar Junction Transistor (BJT) with H-parameter model, Check this book for more knowledge and equations.

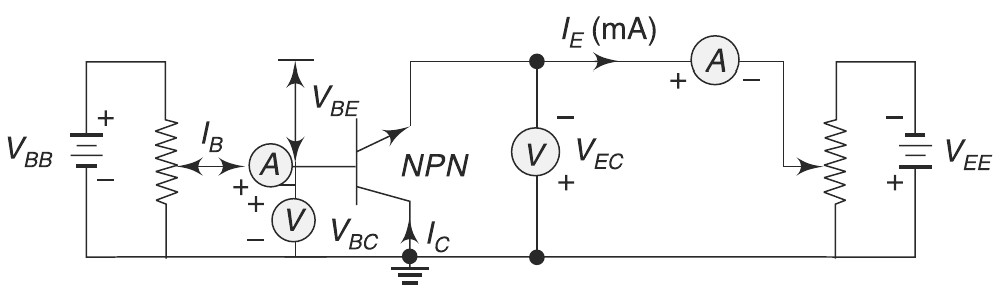
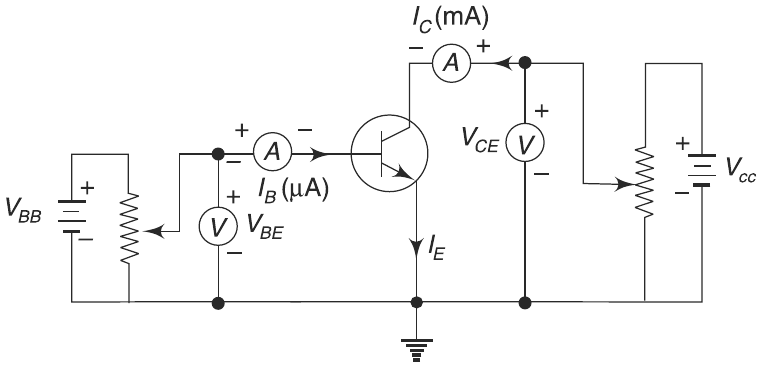
This is the circuit diagram of Common Collector: Small Signal Analysis of BJT

This is the circuit diagram of Common Emmiter:
So the H-Parameter model and its Gain and Impedence are :
Current Gain \(A_i\) = - \(\frac{I_c}{I_b}\)
Voltage Gain \(A_v\) = - \(\frac{A_i * R_l}{Z_i}\)
Input Impedence \(Z_i\) = \(H_ie\) - \(\frac{H_re*H_fe*R_l}{1+H_oe*R_l}\)
Output Impedence \(Z_o\) = \(R_l\)

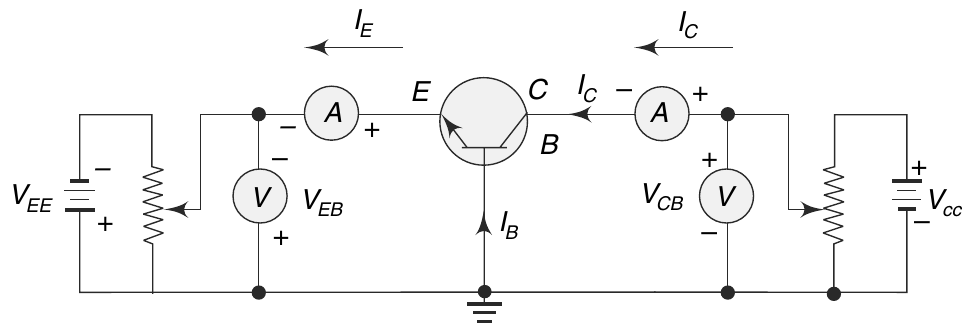
This is the circuit diagram of Common Base: Small Signal Analysis of BJT

Characteristic Model of MOSFET

Characteristic model of Metal-Oxide-Semiconductor Field-Effect Transistor (MOSFET), \[ h_{ib} = \frac{\partial V_{EB}}{\partial I_E} \]

Basics of Control System

Lets consider a example :

Here we know a mechanical system that is damped (bx) and Spring (k) with distance or displacement (x) with Force (F).
The modeling equation of this system is
\[ M \frac{d^2x}{dt^2} + b \frac{dx}{dt} + kx = F \]
Taking the Laplace transform \[ Ms^2X(s) + bsX(s) + kX(s) = F(s) \]
Now the transfer function between the displacement \(X(s)\) and the input \(F(s)\):
\[ \frac{X(s)}{F(s)} = \frac{1}{Ms^2 + bs + k} \]